Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Which of these numbers is not a perfect square: 121, 2, 100, or 4?
|
|
|
2.
|
Which of these numbers is a perfect square: 50, 20, 25, or 15?
|
|
|
3.
|
Which 2 consecutive square numbers is 54 between?
a. | 53 and 55 | b. | 28 and 32 | c. | 49 and 64 | d. | 12 and 16
|
|
|
|
4.
|
The areas of 4 squares are given: 127 cm2, 116 cm2, 121
cm2, and 131 cm2.
Which area is a perfect square?
a. |  cm2 cm2 | b. |  cm2 cm2
| c. | 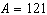 cm2 cm2 | d. |  cm2
cm2 |
|
|
|
5.
|
Find the square of 3.
|
|
|
6.
|
Find the sum of 42 + 92.
|
|
|
7.
|
Simplify 72.
|
|
|
8.
|
The area A of a square is given.
Which side length is a whole
number?
i) A = 57 m2 ii) A = 68 m2 iii)
A = 64 m2 iv) A = 77 m2
|
|
|
9.
|
Find 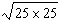 .
|
|
|
10.
|
Which whole number is  closer to?
|
|
|
11.
|
Simplify 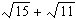 to the nearest whole number.
|
|
|
12.
|
The area of square P is 52 cm2.
Square Q has an area equal to one
quarter the area of square P.
Find the approximate side length of square Q.
Give your answer
to 1 decimal place.
a. | 3.6 cm | b. | 5.1 cm | c. | 13 cm | d. | 1.8
cm |
|
|
|
13.
|
Find the area of the indicated square. 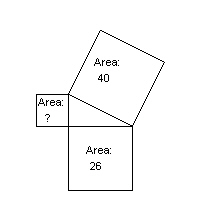 a. | 20 square units | c. | 3.7 square units | b. | 66 square
units | d. | 14 square
units |
|
|
|
14.
|
Find the length of the diagonal, d, in the square. Give your answer to 1
decimal place.  a. | 9 m | b. | 162 m | c. | 18 m | d. | 12.7 m |
|
|
|
15.
|
Use the Pythagorean Theorem to find the area of this square.  a. | 13 square units | b. | 16 square units | c. | 9 square units | d. | 2 square
units |
|
|
|
16.
|
Find the length of the hypotenuse. Give your answer to 1 decimal
place.  a. | 4.7 cm | b. | 7.2 cm | c. | 4.5 cm | d. | 6.3
cm |
|
|
|
17.
|
Ryan owns a plot of land in the shape of a right triangle.
The lengths of
the 2 legs of the plot of land are 15 m and 19 m.
Find the length of the hypotenuse. Round your
answer to the nearest tenth.
a. | 19.4 m | b. | 24.2 m | c. | 11.7 m | d. | 28.7
m |
|
|
|
18.
|
This is an incomplete net for a square pyramid. What shapes do you add to
complete the net? 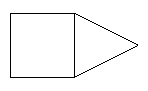 a. | 3 triangles | c. | 1 triangle and 3 squares | b. | 2
squares | d. | 1 triangle and 2
squares |
|
|
|
19.
|
Which diagram is the net for a square pyramid?  a. | Net A | b. | Net B | c. | Net C | d. | Net
D |
|
|
|
20.
|
How many triangular faces are there in a pentagonal pyramid?
|
|
|
21.
|
Identify the polyhedron that has this net.  a. | Rectangular pyramid | c. | Rectangular prism | b. | Triangular pyramid | d. | Triangular
prism |
|
|
|
22.
|
Draw a net for this object. 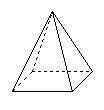
|
|
|
23.
|
The area of one face of a cube is 25 cm2. What is the surface area of
the cube?
a. | 100 cm2 | b. | 100150 cm2 | c. | 30 cm2 | d. | 125
cm2 |
|
|
|
24.
|
Calculate the surface area of this right triangular prism. 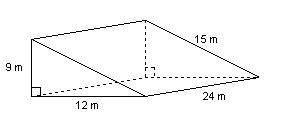 a. | 1080 m2 | b. | 918 m2 | c. | 648 m2 | d. | 972
m2 |
|
|
|
25.
|
The total area of the 3 rectangular faces of a right triangular prism is 56
cm2.
The total surface area of the prism is 68 cm2. Find the area of each
triangular face.
a. | 6 cm2 | b. | 12 cm2 | c. | 1.2 cm2 | d. | 49.3
cm2 |
|
|
|
26.
|
A flower bed measures 1.5 m by 2.4 m and is filled with soil to a depth of 0.6
m.
What is the volume of soil in the flower bed?
a. | 2.16 m3 | b. | 2.34 m3 | c. | 4.5 m3 | d. | 18
m3 |
|
|
|
27.
|
The base of a triangular prism is a right isosceles triangle. Each leg of the
triangle measures 2 cm.
The length of the prism is 8 cm. Find the volume of the prism.
a. | 8 cm3 | b. | 32 cm3
| c. | 4
cm3 | d. | 16 cm3 |
|
|
|
28.
|
Use this net to find the surface area of the cylinder. Give the answer to the
nearest square metre. 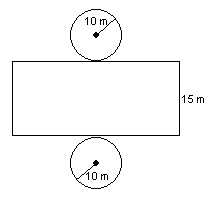  a. | 785 m2 | b. | 1257 m2 | c. | 1100 m2 | d. | 1571
m2 |
|
|
|
29.
|
Find the surface area of this cylinder to the nearest square metre.  a. | 905 m2 | b. | 704 m2 | c. | 653 m2 | d. | 452
m2 |
|
|
|
30.
|
Tamara needs to buy motor oil to fill the 5 empty cylindrical barrels at her oil
service center. Each barrel is 3.0 m deep and has radius 1.5 m. What is the volume of oil needed?
Use 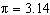 and give your answer to the nearest hundredth. a. | 84.78 m3 | b. | 423.9 m3 | c. | 141.3 m3 | d. | 105.98
m3 |
|
Short Answer
|
|
|
31.
|
Which 2 consecutive square numbers is 126 between?
|
|
|
32.
|
Find 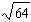 .
|
|
|
33.
|
Copy the square on grid paper. Find its area. Then write the side length
of the square. 
|
|
|
34.
|
Square A has area 10 cm2.
Square B has area double that of square
A.
What is the side length of square B? Give your answer to the nearest centimetre.
|
|
|
35.
|
A boat sails due south from a port at a steady speed of 9 km/h.
The wind
blows the boat due west at a speed of 3 km/h.
How far is the boat from the port after 1 h?
Give your answer to 1 decimal place.
|
|
|
36.
|
The net for a cereal box is shown. Describe the shape and dimensions of the
box. 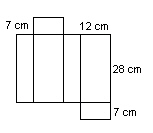
|
|
|
37.
|
The length of one edge of a cube is 4 cm. a) Find the surface area of the
cube.
b) Find the new surface area if the edge length is multiplied
by 3.
c) What is the ratio of the new surface area to the surface
area in part a?
|
|
|
38.
|
Find the surface area of this right triangular prism. 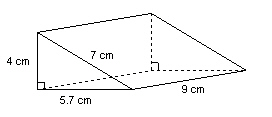
|
|
|
39.
|
The area of a rectangular face of an equilateral triangular prism is 21
cm2.
No dimension can be 1 cm. What are the possible whole-number dimensions of the
edges?
|
|
|
40.
|
Here is the net of a right triangular prism. The area of each face, in square
centimetres, is given. Find the surface area of the prism formed from this net. 
|
|
|
41.
|
Here is a right triangular prism. a) Find the surface area of the
prism.
b) If all the dimensions of the prism are doubled, what is
the new surface area?
c) How does this new surface area compare to
the original surface area?
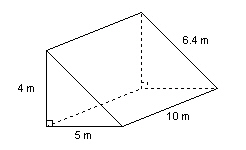
|
|
|
42.
|
The length of one edge of a cube is 5 cm. a) Find the volume of the
cube.
b) Find the new volume if the edge length is multiplied by
2.
c) What is the ratio of the new volume to the volume in part
a?
|
|
|
43.
|
If each of the length, width, and height of a rectangular prism is doubled, what
happens to the volume?
|
|
|
44.
|
Calculate the volume of this triangular prism. 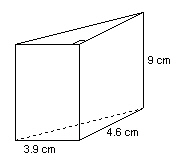
|
|
|
45.
|
The rectangular prism has dimensions 14 cm, 9 cm, and 7 cm. It is divided
into 2 congruent triangular prisms along the diagonal shown. Find the volume of each triangular
prism. 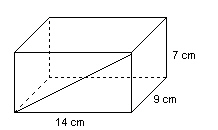
|
|
|
46.
|
Which cylinder has the greatest surface area?
Cylinder A: base radius 3 cm,
length 5 cm
Cylinder B: base radius 4 cm, length 3 cm
Cylinder C: base radius 5 cm, length 1
cm
Cylinder D: base radius 3 cm, length 6 cm
|
|
|
47.
|
This object is made using 6 linking cubes. Sketch the front and side views of
the object. 
|
|
|
48.
|
The top and bottom of this object are squares. Sketch the top and front views of
the object. 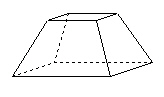
|
|
|
49.
|
This object is made using linking cubes. Sketch the top, front, left side, and
right side views of the object. 
|
|
|
50.
|
These are the top, front, and right side views of an object built using linking
cubes. Sketch a 3-D picture of the object. 
|
Problem
|
|
|
51.
|
The numbers 2, 3, 5, 7, 11, and 13 are written on separate cards.
Which
pairs of numbers give a sum that is a perfect square?
Find all possible solutions.
|
|
|
52.
|
The 2 diagonals of rhombus PQRS measure 10 cm and 14 cm. The diagonals intersect
at T. Find the side length of the rhombus. Justify your answer. 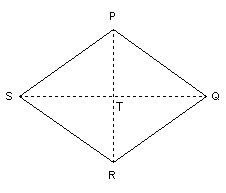
|
|
|
53.
|
The diagram is a partially drawn net with three equilateral
triangles. Describe with dimensions the additional shape(s) required to complete the net for each
object. a) a triangular
pyramid
b) a square pyramid
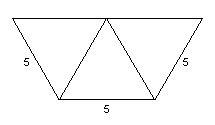
|
|
|
54.
|
Sketch the object that can be made from this net. 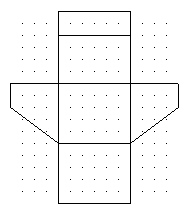
|
|
|
55.
|
A cube is made from 125 centimetre cubes. What is the surface area of the
cube?
|
|
|
56.
|
The volume of a piece of metal is 24 cm 3. It is melted and cast into
the shape of a rectangular prism. a)
What are the possible whole number dimensions of the metallic prism in
centimetres?
b) The metallic prism is plated with a thin layer of
gold. What are the dimensions of the prism that requires the least amount of gold?
|
|
|
57.
|
A cylinder has radius 4 cm and height 7 cm. A cube has edge length 8 cm.
Would either solid fit inside the other? Explain.
|
|
|
58.
|
Sketch 3 views of this object. 
|
|
|
59.
|
This object is built using linking cubes. Sketch 2 possible top views of this
object. 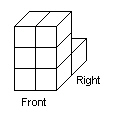
|
|
|
60.
|
These are the 3 views of an object built using linking cubes. Sketch the
object. 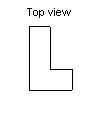 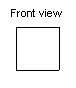 
|