Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
A bank surveyed its loans to new small businesses. It found that the ratio of
unpaid or overdue loans to good loans was 2:4. If 330 small businesses are selected randomly from the
bank’s files, how many are likely to have unpaid or overdue loans?
|
|
|
2.
|
Kelly works in the library and earned $58 last week. She spent $39 on a video
game and saved the rest. Write the ratio of the money saved to the money earned in two ways.
a. | 39:19 and 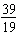 | c. | 58:19 and 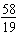 | b. | 39:58 and 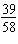 | d. | 19:58 and 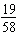 |
|
|
|
3.
|
The ratio of the three sides of a right triangle is equivalent to the ratio of
the corresponding sides of a similar triangle. The ratio is 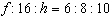 . Determine the unknown
measures f and h.  Diagram not to scale Diagram not to scale
|
|
|
4.
|
Each week, Joy drives 145 km for work and uses approximately 12 L of gasoline.
What is her car’s rate of fuel consumption in litres per 100 km?  a. | 8.3 L/100 km | c. | 4.2 L/100 km | b. | 0.1 L/100 km | d. | 1.2 L/100 km |
|
|
|
5.
|
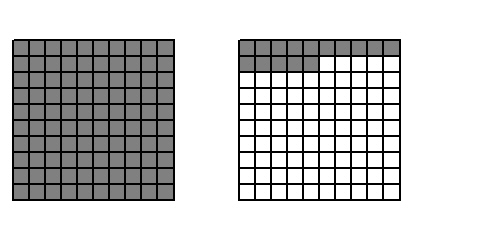
One completely shaded grid represents 100%. What percent does this diagram
represent?
|
|
|
6.
|
Five-sevenths of a percent of the volume of apple juice in a container is
approximately 10.36 mL. What is the total volume of apple juice in the container?
a. | 145.00 L | c. | 1.45 L | b. | 14.50 L | d. | 0.15 L |
|
|
|
7.
|
A remote village in British Columbia had a population of 293 in 2014. The
population decreased by 5.5% in 2015 and increased by 3.3% in 2016. What is the village’s
population at to start 2017?
|
|
|
8.
|
Write a proportion to determine 15% of 12. Solve the proportion to determine
this number, n.
a. | 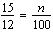 ; n = 125 ; n = 125 | c. | 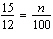 ; n =
12.5 ; n =
12.5 | b. | 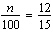 ; n = 0.18 ; n = 0.18 | d. | 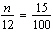 ; n =
1.8 ; n =
1.8 |
|
|
|
9.
|
Jamie earns $4400 per month. He spends $2024 on rent and his car loan. What
percent of his income does Jamie spend on rent and his car loan?
|
|
|
10.
|
A square has an area of 144 cm2. What is the side length of the
square?
a. | 12 cm | c. | 288 cm | b. | 6 cm | d. | 20736 cm |
|
|
|
11.
|
Represent the Pythagorean relationship symbolically using the triangle
shown. 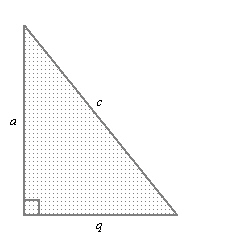
|
|
|
12.
|
The value of 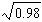 is approximately _________.
|
|
|
13.
|
A square has an area of 81 cm2. Find the side length of the square.
Round your answer to the nearest tenth of a centimetre.
a. | 9.0 cm | c. | 6.4 cm | b. | 12.7 cm | d. | 20.3 cm |
|
|
|
14.
|
If only the two ends of the roof area need to be painted, what is the total
surface area that needs to be painted? Round your answer to the nearest tenth of a metre. 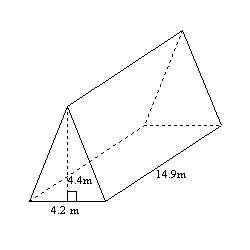 Diagram not drawn to
scale Diagram not drawn to
scalea. | 36.3 m2 | b. | 18.5 m2 | c. | 72.6 m2 | d. | 9.2
m2 |
|
|
|
|
|
|
15.
|
Given the four views of the same die, how many dots will be found on the bottom
face of this die?

|
|
|
16.
|
To find the surface area of a cube, you must know the dimensions of
__________.
a. | 2 faces | c. | 3 faces | b. | 4 faces | d. | 1 face |
|
|
|
17.
|
What is the surface area of the two bases of a cylinder with a radius of 2 cm
and a height of 12 cm? 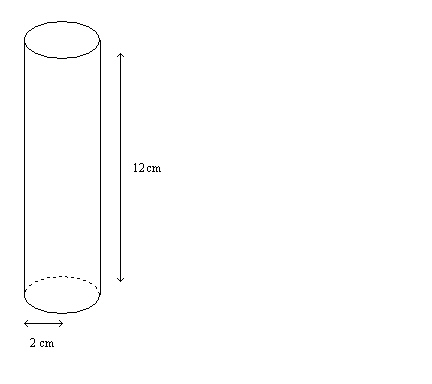 a. | 150.80 cm2 | c. | 25.13 cm2 | b. | 12.57cm2 | d. | 100.53
cm2 |
|
|
|
18.
|
This object is made from 7 centimetre cubes. What is its surface area?  a. | 26 cm2 | c. | 15 cm2 | b. | 30 cm2 | d. | 24
cm2 |
|
|
|
19.
|
What is the cube root of 512?
a. | 134 217 728 | c. | 24 | b. | 1536 | d. | 8 |
|
|
|
20.
|
Which of the following whole numbers has a cube root between 4 and 5?
|
|
|
21.
|
Aria calculates the volume of a gift box measuring 35 cm  30 cm  20
cm. Her answer will be expressed in __________. a. | quadratic centimetres | c. | cubic centimetres | b. | centimetres | d. | square
centimetres |
|
|
|
22.
|
What is the volume of the cylinder, rounded to the nearest cubic inch?  Diagram not drawn to
scale Diagram not drawn to
scale
a. | 9 in.3 | c. | 37 in.3 | b. | 18 in.3 | d. | 27
in.3 |
|
|
|
23.
|
The volume of this triangular prism would be calculated as 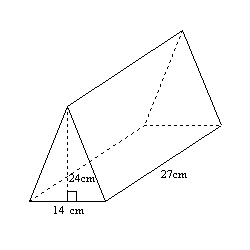 Diagram not drawn to
scale Diagram not drawn to
scale
|
|
|
Choose the best answer.
|
|
|
24.
|
Which multiplication statement represents the following addition statement?
4
+ 4 + 4 + 4
a. | 2 ´ 4 | c. | 4 ´
44 | b. | 4 ´ 4 | d. | 44 ´
44 |
|
|
|
25.
|
When you multiply an odd number of negative integers by an odd number of
positive integers, what type of integer do you always get?
a. | infinite integer | c. | positive integer | b. | negative integer | d. | zero |
|
|
|
26.
|
Which expression does this diagram represent? 
|
|
|
27.
|
A stock decreased in price by $60 over five days. Determine the mean daily
decrease in price.
a. | $5/day | c. | $20/day | b. | $12/day | d. | $30/day |
|
|
|
28.
|
A pilot is flying at an altitude of 6000 m, where the temperature is -23 °C. As the plane descends toward the
airport, the temperature increases by 2 °C for every 1000 m drop in
elevation. The airport is at an elevation of 1000 m. What is the temperature there?
a. | -11 °C | c. | -13 °C | b. | -12 °C | d. | -14 °C |
|
|
|
29.
|
Determine the result of 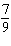 - - 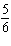 , in
lowest terms.
|
|
|
30.
|
Express the result of 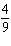 - - 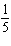 +
+ 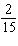 , in lowest terms.
|
|
|
31.
|
|
|
|
32.
|
Calculate 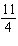 - - 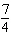 - - 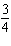 and express the answer in lowest terms.
|
|
|
33.
|
Determine 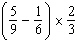 . Express your answer in lowest terms.
|
|
|
34.
|
Calculate 2 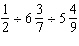 .
|
|
|
35.
|
The total area of Canada is about 9 985 000 km 2. The total area of
Nova Scotia is about 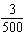 of the total area of Canada. What is the area of Nova
Scotia? a. | 16 641 667 km2 | c. | 599 100
km2 | b. | 1 664 167 km2 | d. | 59 910 km2 |
|
|
|
36.
|
Calculate 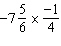 .
|
|
|
37.
|
For the equation 2x – 1 = 10, which operation should you use in
isolating the variable?
a. | addtion | c. | multiplication | b. | division | d. | subtraction |
|
|
|
38.
|
The phrase “9 times a number, increased by 12, equals 15” can be
modelled with the equation
|
|
|
39.
|
What is the solution to the equation 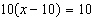 ?
|
|
|
40.
|
What is the solution to the equation 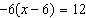 ?
|
|
|
Benjamin drives from Vancouver to Nelson. The total distance is 660 km,
which took 7.5 hours to drive. He uses a table to record the data. Time t (h) | Distance d (km) | 1.1 | 94 | 2.1 | 189 | 3.2 | 283 | 4.3 | 377 | 5.4 | 471 | 6.4 | 566 | 7.5 | 660 | | |
|
|
|
41.
|
What graph represents the linear relation?
|
|
|
42.
|
How far did Benjamin drive in the first 3.1 hours?
a. | 583 km | c. | 292 km | b. | 386 km | d. | 197 km |
|
|
|
Study this growing pattern of hexagons. 
|
|
|
43.
|
What linear relation shows the relationship between the number of line segments,
l, and the number of hexagons, h?
|
|
|
Study this growing pattern of octagons. 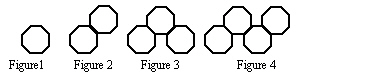
|
|
|
44.
|
What would be the number of line segments, l, when the number of octagons
is 14?
|
|
|
Study this growing pattern of rhombuses. 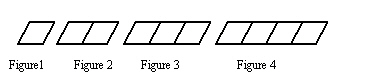
|
|
|
45.
|
What graph shows the relationship between the number of line segments, l,
and the number of rhombuses, r?
|
|
|
Study this growing pattern of rhombuses. 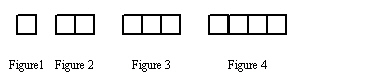
|
|
|
46.
|
What linear relation shows the relationship between the number of line segments,
l, and the number of squares, s?
a. | l = 4 + s | c. | l = 2s - 2 | b. | l = 4s –
1 | d. | l = 2s +
2 |
|
|
|
47.
|
Zoe’s percent midterm marks for six courses are 90, 65, 77, 89, 75, 90.
What is her mean mark?
|
|
|
48.
|
A school hockey team scored 9, 2, 4, 9, 6, 7, 5 goals in seven regular season
games. Which two measures of central tendency have the same value?
a. | mean and range | c. | mean and mode | b. | median and mean | d. | median and mode |
|
|
|
Rawan is doing a school project where she has to exercise every day of the
week. The table shows how long she exercised each day last week. Day of the Week | Exercise Time (min) | | Monday | 27 | | Tuesday | 27 | | Wednesday | 25 | | Thursday | 27 | | Friday | 26 | | Saturday | 49 | | Sunday | 29 | | |
|
|
|
49.
|
Which is the best measure of central tendency for Rawan’s data set?
a. | median | c. | range | b. | mean | d. | mode |
|
|
|
50.
|
Every day, Rawan goes to a restaurant for lunch. She orders a salad and a soup,
at random. There are 6 different salad choices and 4 different soup choices. If she has a different
lunch each day, how long will it take for her to have tried all of the possible combinations?
a. | 10 days | c. | 6 days | b. | 24 days | d. | 35 days |
|