Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Determine the value of x if 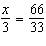 .
|
|
|
2.
|
If there are 104 flights a day in and out of Kelowna airport, and 10% of the
flights are late, approximately many flights will arrive on time?
|
|
|
3.
|
The ratio of the three sides of a right triangle is equivalent to the ratio of
the corresponding sides of a similar triangle. The ratio is 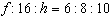 . Determine the unknown
measures f and h. 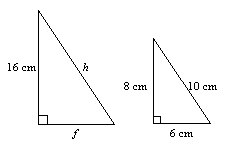 Diagram not to scale Diagram not to scale
|
|
|
4.
|
Oranges are sold at $1.09 per kilogram. Mohan buys 13 kg of oranges. Determine
how much he pays.
a. | $14.17 | c. | $15.17 | b. | $13.67 | d. | $14.67 |
|
|
|
5.
|
One completely shaded grid represents 100%. Which grid represents 100 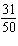 %?
|
|
|
6.
|
How many hundred grids do you need to represent 764%?
|
|
|
7.
|
Express 6.75 as a mixed number in lowest terms.
|
|
|
8.
|
Write a proportion to determine 15% of 12. Solve the proportion to determine
this number, n.
a. |  ; n = 125 ; n = 125 | c. | 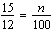 ; n =
12.5 ; n =
12.5 | b. |  ; n = 0.18 ; n = 0.18 | d. |  ; n =
1.8 ; n =
1.8 |
|
|
|
9.
|
Harry buys a laptop for $749.99. In his province, the sales tax is 15%. How much
does Harry pay for the laptop with tax? Express your answer to the nearest 5 ¢.  a. | $637.50 | c. | $862.50 | b. | $112.50 | d. | $806.25 |
|
|
|
10.
|
The areas of the squares shown are in square centimetres. Use the Pythagorean
relationship to find the unknown area of the square.
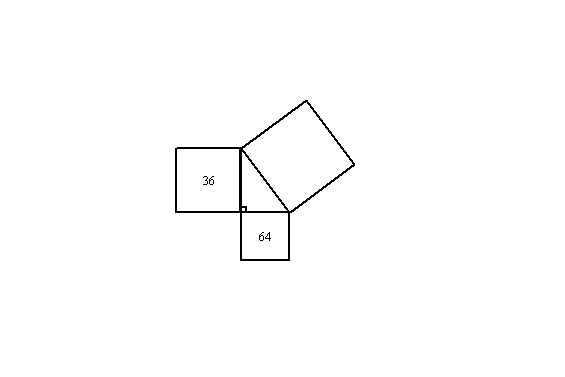 a. | 14 cm2 | c. | 100 cm2 | b. | 2304 cm2 | d. | 48
cm2 |
|
|
|
11.
|
The value of 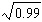 is between which two numbers? a. | 1 and 1.01 | c. | 0.98 and 0.99 | b. | 1.01 and
1.02 | d. | 0.99 and
1 |
|
|
|
12.
|
Determine the approximate area of the square that can be drawn on the missing
side. 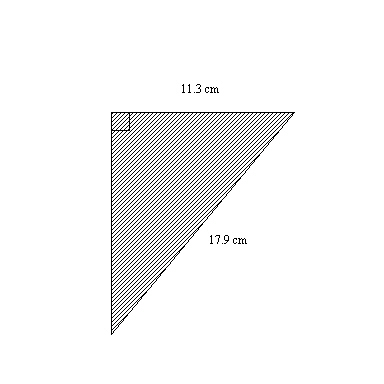 a. | 448.1 cm2 | c. | 192.7 cm2 | b. | 43.6 cm2 | d. | 202.3
cm2 |
|
|
|
13.
|
The hypotenuse of a right triangle is 26 cm. One leg of the triangle is 12 cm.
How long must the other leg be, to the nearest tenth of a centimetre?
a. | 23.1 cm | c. | 196.0 cm | b. | 14.0 cm | d. | 28.6 cm |
|
|
|
14.
|
What is the minimum number of views needed to describe a 3-D object?
|
|
|
15.
|
Find the surface area of this rectangular prism.
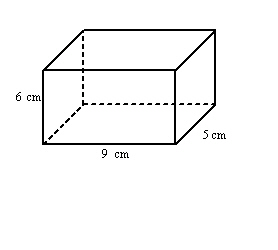 a. | 258 cm2 | c. | 270 cm2 | b. | 135 cm2 | d. | 129
cm2 |
|
|
|
16.
|
What 3-D object can be created by folding this net? 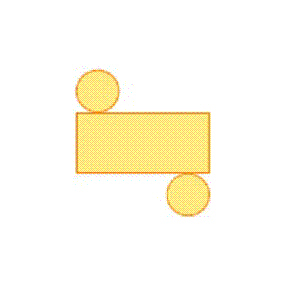 a. | rectangular prism | c. | cylinder | b. | triangular prism | d. | cube |
|
|
|
17.
|
The distance between adjacent dots (vertical and horizontal) is 2 cm. What would
be the surface area of the 3-D object produced by the net shown? 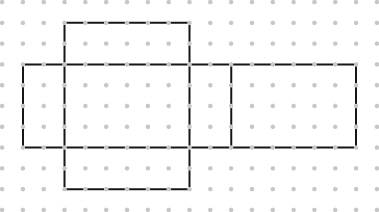 a. | 88 cm2 | c. | 176 cm2 | b. | 96 cm2 | d. | 24
cm2 |
|
|
|
18.
|
What is the surface area of a cylinder with a radius of 3 cm and a height of 19
cm, to the nearest hundredth of a square centimetre?
a. | 395.84 cm2 | c. | 56.55 cm2 | b. | 414.69 cm2 | d. | 358.14
cm2 |
|
|
|
19.
|
The value of 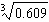 is between which two numbers? a. | 0.847 and 0.848 | c. | 0.848 and 0.849 | b. | 0.849 and 0.85 | d. | 0.846 and 0.847
|
|
|
|
20.
|
The volume of a cube with side lengths of 7 cm is __________.
a. | 49 cm3 | c. | 2401 cm3 | b. | 343 cm3 | d. | 7
cm3 |
|
|
|
21.
|
Which rectangular prism has the greatest surface area to volume ratio? 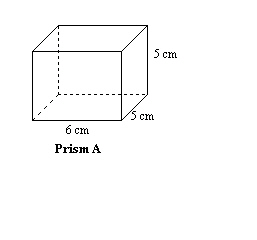 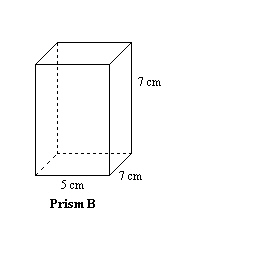 a. | Prism A | c. | They have the same ratio. | b. | Prism
B | d. | There is not enough
information to calculate the ratios. |
|
|
|
22.
|
Determine the volume of the right triangular prism. 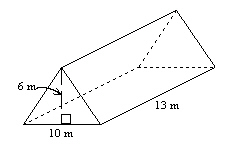 Diagram not drawn to
scale Diagram not drawn to
scalea. | 180 m3 | c. | 360 m3 | b. | 780 m3 | d. | 390
m3 |
|
|
|
23.
|
A rectangular-based prism has a base area of 16 cm 2 and a height of
12 cm. What is the volume of a pyramid that has a congruent base and the same height as the
prism? 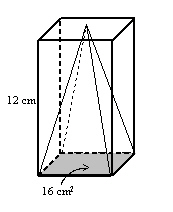 Diagram not drawn to scale Diagram not drawn to scalea. | 48 cm3 | c. | 96 cm3 | b. | 192 cm3 | d. | 64
cm3 |
|
|
|
24.
|
Determine which multiplication statement this diagram represents. 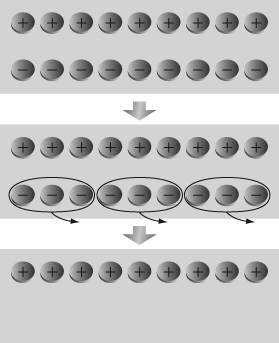
|
|
|
25.
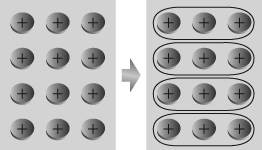
|
What division statement does this diagram represent?
|
|
|
26.
|
Martina improved her math mark by 2% on each of six tests. How much higher was
her mark on the last test than on the first?
|
|
|
27.
|
Evaluate –8 – 3(–2 – 1).
|
|
|
28.
|
Blaine drove from Calgary to Winnipeg at an average speed of 90 km/h. After 11
hours Blaine was 218 km from Winnipeg. Determine how far apart Calgary and Winnipeg are from one
another.
a. | 772 km | c. | 1208 km | b. | 990 km | d. | 1306 km |
|
|
|
29.
|
What fraction, in lowest terms, is shown by the shaded parts of the
diagram? 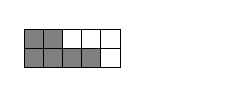
|
|
|
30.
|
What is 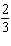 + + 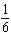 , in lowest terms?
|
|
|
31.
|
What is 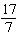 when it is written as a mixed number?
|
|
|
32.
|
Calculate 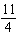 - -  - - 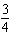 and express the answer in lowest terms.
|
|
|
33.
|
Determine  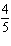 , in lowest terms.
|
|
|
34.
|
Calculate 2 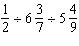 .
|
|
|
35.
|
Olivia spends half an hour each night working on Math. This is 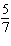 as much time
as she spends on English. How much time does she spend on English?
|
|
|
36.
|
Calculate  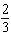 .
|
|
|
37.
|
The total delivery cost on a shipment of furniture is 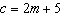 , where
m represents the number of pieces of furniture being delivered, and c is the total
cost. How much would it cost to deliver eight pieces of furniture? a. | $38.00 | c. | $21.00 | b. | $11.00 | d. | $42.00 |
|
|
|
38.
|
Solve the equation 2y – 6 = 38.
|
|
|
39.
|
Thomas has scored 37 points in 9 hockey games this season. His goal for the
season is to score 60 points. Which equation can be used to find the number of points, p, that
Thomas must average in his last six games to reach his goal?
a. | 37 – 6p = 60 | c. | 60 + 6p =
37 | b. | 37p + 6= 60 | d. | 37 + 6p = 60 |
|
|
|
40.
|
The phrase “9 times a number, increased by 12, equals 15” can be
modelled with the equation
|
|
|
41.
|
Madison purchased 7 DVDs. The tax on each DVD was $4; the total cost was $146.
What equation models this situation?
|
|
|
42.
|
Sophia purchased 5 DVDs. The tax on each DVD was $1; the total cost was $135.
What was the cost of each DVD?
|
|
|
Benjamin drives from Vancouver to Nelson. The total distance is 660 km,
which took 7.5 hours to drive. He uses a table to record the data. Time t (h) | Distance d (km) | 1.1 | 94 | 2.1 | 189 | 3.2 | 283 | 4.3 | 377 | 5.4 | 471 | 6.4 | 566 | 7.5 | 660 | | |
|
|
|
43.
|
How long did it take Benjamin to drive 389 km?
a. | 1.2 h | c. | 3.1 h | b. | 4.1 h | d. | 0.2 h |
|
|
|
Study this growing pattern of hexagons. 
|
|
|
44.
|
What graph shows the relationship between the number of line segments, l,
and the number of hexagons, h?
|
|
|
Study this growing pattern of octagons. 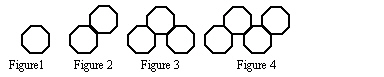
|
|
|
45.
|
What linear relation shows the relationship between the number of line segments,
l, and the number of octagons, g?
|
|
|
46.
|
What is the solution to the equation 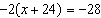 ?
|
|
|
47.
|
A meteorologist wants to determine how much snow a city receives in a year.
Which measure of central tendency is the most appropriate to use?
a. | median | c. | mode | b. | mean | d. | range |
|
|
|
48.
|
Which measure of central tendency is always equal to one of the values in the
data set?
a. | range | c. | mean | b. | median | d. | mode |
|
|
|
Rawan is doing a school project where she has to exercise every day of the
week. The table shows how long she exercised each day last week. Day of the Week | Exercise Time (min) | | Monday | 27 | | Tuesday | 27 | | Wednesday | 25 | | Thursday | 27 | | Friday | 26 | | Saturday | 49 | | Sunday | 29 | | |
|
|
|
49.
|
What is the value of the outlier in Rawan’s data set?
|
|
|
50.
|
How many possible outcomes are there when you flip a coin and roll a
twenty-sided die at the same time?
|