Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Use this balance-scales model to solve for x. 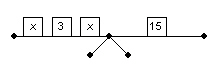
|
|
|
2.
|
In the left pan of a set of balance-scales, there are 2 identical unknown masses
and a mass of 18 g.
The scales are balanced by adding a mass of 24 g to the right pan.
Find
the value of each unknown mass.
|
|
|
3.
|
Write an equation for this sentence.
4 added to 4 times a number is 57.
a. | 4 + 4 = 57x | c. | 4 - 4x = 57 | b. | 4 + 4x =
57 | d. | 4x + 4 =
57 |
|
|
|
4.
|
Write an equation for this situation.
Each of 5 people contributed $y
to buy a gift that costs $20.
|
|
|
5.
|
Solve this equation. –26 + 2x = –2
|
|
|
6.
|
Solve this equation. 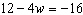
|
|
|
7.
|
Solve this equation. 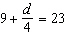
|
|
|
8.
|
Evaluate. 2(5 + 8)
|
|
|
9.
|
Expand. 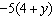
|
|
|
10.
|
Which statement is correct?
|
|
|
11.
|
Solve this equation: 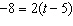
|
|
|
12.
|
Complete this table of values for the relation 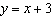 . 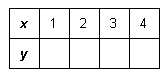
|
|
|
13.
|
Complete this table of values for the relation 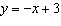 . 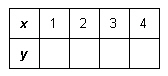
|
|
|
14.
|
Complete this table of values for the relation 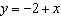 . 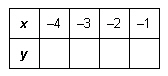
|
|
|
15.
|
Describe the relationship between the variables x and y in this
graph. Graph of 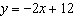 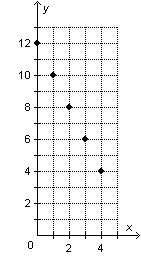 a. | When x increases by 1, y decreases by 12. | b. | When x
increases by 1, y decreases by 2. | c. | When x increases by 1, y
increases by 2. | d. | When x increases by 2, y increases by
12. |
|
Short Answer
|
|
|
16.
|
Use this balance-scales model to solve for x. 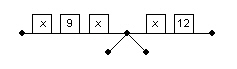
|
|
|
17.
|
Miranda opened a checking account with $560. She withdrew the same amount each
week for 13 weeks. Her balance was then $365. a) Write an equation you can use to find how
much money Miranda withdrew each week.
b) Solve the equation and
solve the problem.
|
|
|
18.
|
Solve this equation. 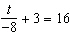
|
|
|
19.
|
Write an equation for this sentence, then solve the equation.
When 7 is
subtracted from a number divided by 3, the result is 14.
|
|
|
20.
|
Write an equation for this sentence, then solve the equation.
When a number
divided by 5 is subtracted from 13, the result is 8.
|
|
|
21.
|
Match each expression in Column 1 with an equivalent expression in Column
2. Column 1 Column 2
a) 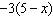 i) 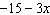
b) 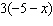
ii) 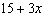
c) 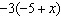 iii) 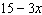
d) 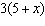
iv) 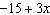
|
|
|
22.
|
Ms. Jones pays for 4 teens to go to a local theatre and supplies each with a
snack. The admission cost for a teen is $11 and a snack costs $9. a) Write 2 different expressions to find the
total cost of the outing.
b) How much does Ms. Jones have to
pay?
|
|
|
23.
|
The equation of a linear relation is 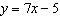 . What is the value of y when
x = 2?
|
|
|
24.
|
The equation of a linear relation is 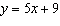 . What is the value of x when
y = 34?
|
|
|
25.
|
Make a table of values for the relation 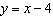 for x = –4,
–3, –2, –1, 0.
|
|
|
26.
|
Make a table of values for the relation 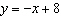 for integer values of
x from –3 to 3.
|
|
|
27.
|
Harry has $110 in his savings account. He decides to save $15 every month to buy
a bike. An equation for this relation is 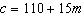 , where c represents the amount
of money, in dollars, in his account and m represents the number of months. How many months
does it take Harry to have $185 in his account?
|
|
|
28.
|
The graph shows the relation 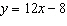 . Write the ordered pair for point
P. 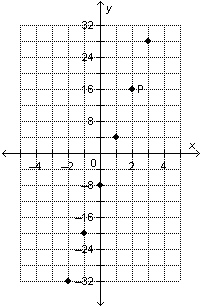
|
|
|
29.
|
The graph shows the relation 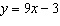 . Write the ordered pair for point
Q. 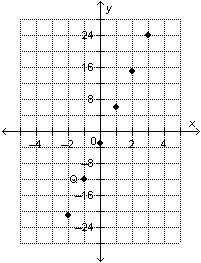
|
|
|
30.
|
Graph the relation 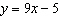 for integer values of x from -4 to 4.
|
Problem
|
|
|
31.
|
Sketch a balance-scales model to represent this equation: 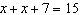 Solve the
equation for x. Show your work.
|
|
|
32.
|
You have 3 known masses: 1 kg, 3 kg, and 5 kg. Show how you can use these
masses and balance scales to find an unknown mass of 1 kg to 9 kg. Use this table to
help. Left Pan | Right
Pan | Unknown
Mass | Known Mass | Known
Mass | 1
kg | | | 2
kg | | | 3
kg | | | 4
kg | | | 5
kg | | | 6
kg | | | 7
kg | | | 8
kg | | | 9
kg | | | | | |
|
|
|
33.
|
You have two x-tiles, 5 positive unit tiles, and 3 negative unit
tiles.
Use these tiles to model 3 different equations with the solution x = 3.
The two
x-tiles must be used each time.
|
|
|
34.
|
I think of a number, divide it by 6, then add 4.
If the result is 17, what
is the original number?
Explain your work.
|
|
|
35.
|
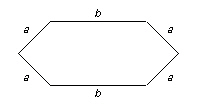
a) Write a formula
for the perimeter, P, of this hexagon 2 different ways.
b)
Find the perimeter of the hexagon when a = 4 cm and b = 8 cm.
|
|
|
36.
|
Solve this equation: 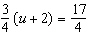 Show your work.
|
|
|
37.
|
Make a table of values for the relations 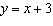 and 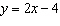 . For what
value of x will the relations have the same y-value?
|
|
|
38.
|
This table of values is for the linear relation with equation 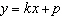 , where
k and p are constants. Find the values of k and p. Show your
method. 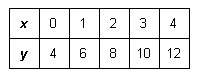
|
|
|
39.
|
a) Graph both
relations on the same coordinate axes.
i) 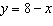
ii) 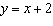 b) Find the ordered
pair on the graph that are in both relations.
|
|
|
40.
|
Patricia makes and sells cards. The cost of producing a set of cards is $210
and each card sells for $11. If s represents the number of cards sold and p
represents Patricia’s profit in dollars, an equation for this relation is 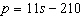 . a) Make a table of values for s = 0, 5,
10, 15, 20, and 25.
b) What does a negative value of p
mean?
c) What is Patricia’s profit if she sells 50 of the set
of cards?
|