Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Four more than three times a number is 16. Let n represent the number.
Solve for n.
|
|
|
2.
|
Write an equation for this sentence.
40 less than a number is 10.
|
|
|
3.
|
Write an equation for this situation.
Each of 5 people contributed $y
to buy a gift that costs $20.
|
|
|
4.
|
Write an equation for this sentence.
A number divided by 4 is 11.
|
|
|
5.
|
Solve this equation. 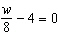
|
|
|
6.
|
Evaluate. 2(5 + 8)
|
|
|
7.
|
Evaluate. 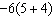
|
|
|
8.
|
Expand. 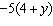
|
|
|
9.
|
Solve this equation: 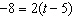
|
|
|
10.
|
Solve this equation: 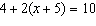 a. | 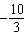 | b. | –2 | c. | 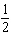 | d. | –4 |
|
|
|
11.
|
Complete this table of values for the relation 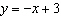 . 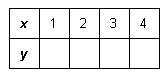
|
|
|
12.
|
Graph the relation y = –2x + 3 for integer values of
x from 0 to 4.
|
|
|
13.
|
Describe the relationship between the variables x and y in this
graph. Graph of 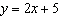 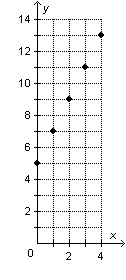 a. | When x increases by 1, y increases by 2. | b. | When x
increases by 1, y increases by 5. | c. | When x increases by 1, y
increases by 7. | d. | When x increases by 2, y decreases by
5. |
|
|
|
14.
|
Complete the table of values for the linear relation 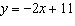 . 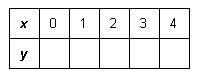
|
|
|
15.
|
Which relations have graphs that are lines going up to the right? a. | ii and iv | b. | i and iii | c. | ii | d. | i, ii, and
iv |
|
Short Answer
|
|
|
16.
|
In the left pan of a set of balance scales, there are 3 identical unknown masses
and a mass of 5 g.
The scales are balanced by placing a mass of 20 g in the right pan.
Find
each unknown mass.
|
|
|
17.
|
Solve this equation. 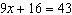
|
|
|
18.
|
Solve this equation. 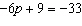
|
|
|
19.
|
Jacqui has $56 in her savings account. She saves $25 each week.
How long
will it take before she has $406 in her account?
Write an equation, then solve the problem.
|
|
|
20.
|
Ivan wants to buy a skateboard that costs $45. He plans to save $3 per week.
How many weeks will it take him to save $45? a) Write an equation you can use to find how
many weeks it will take Ivan to save $45.
b) Solve the equation and
answer the question.
|
|
|
21.
|
Miranda opened a checking account with $560. She withdrew the same amount each
week for 13 weeks. Her balance was then $365. a) Write an equation you can use to find how
much money Miranda withdrew each week.
b) Solve the equation and
solve the problem.
|
|
|
22.
|
Write an equation for this sentence, then solve the equation.
A number
divided by -7 is -8.
|
|
|
23.
|
Which pairs of expressions are equivalent? a) 9(q + 2) and 9q +
2
b) 7(t + 5) and 7t +
35
c) 8(y + 3) and 8y +
11
d) 9(x + 5) and 9x + 45
|
|
|
24.
|
Write a formula for the perimeter, P, of this hexagon 2 different
ways. 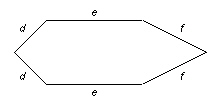
|
|
|
25.
|
Solve this equation: 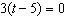
|
|
|
26.
|
Saja and 10 friends went to a fair. The cost of admission was $8 per person.
They each bought an unlimited midway ride ticket. The total cost of admission and ride
tickets for Saja and her friends was $319. What was the price of an unlimited ride
ticket? a) Write an equation to model
the problem.
b) Solve the equation and answer the
question.
|
|
|
27.
|
Make a table of values for the relation 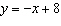 for integer values of
x from –3 to 3.
|
|
|
28.
|
The graph shows the linear relation 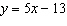 . Describe the relationship between
the variables x and y. 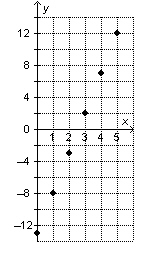
|
|
|
29.
|
Graph the relation 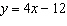 for integer values of x from 0 to 5. Describe the
relationship between the variables x and y in the graph.
|
|
|
30.
|
Graph the relation 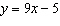 for integer values of x from -4 to 4.
|
Problem
|
|
|
31.
|
Sketch a balance-scales model to represent this equation: 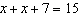 Solve the
equation for x. Show your work.
|
|
|
32.
|
Describe how you model the equation 3x + 7 = 31 using
balance-scales.
Use the model to solve the equation for x.
|
|
|
33.
|
You are a member of a movie club. Every time you see a movie, you earn 2
advantage points.
When you earn 100 points, you get a free movie ticket. Now you have 64
advantage points.
Write an equation to show the number of movies you have to watch before
you earn a free movie ticket.
|
|
|
34.
|
Keith went to a garden centre and bought some potting soil for $13 and 6 shrubs.
If the total cost was $67, how much did each shrub cost if they were priced the same?
Write
an equation you can use to solve the problem. Verify the solution.
Show your work.
|
|
|
35.
|
A student’s work is shown. Check this student’s work. Rewrite a
correct algebraic solution where necessary. 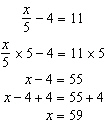
|
|
|
36.
|
I think of a number, divide it by 6, then add 4.
If the result is 17, what
is the original number?
Explain your work.
|
|
|
37.
|
The length of each side of an equilateral triangle is increased by 5 cm. The
perimeter of the new triangle is 72 cm. What was the side length of the original triangle? a) Write an equation that can be solved using
the distributive property.
b) Solve the equation and verify the
solution.
|
|
|
38.
|
Make a table of values for the relation 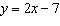 for integer values of
x from –3 to 3. a) Find
the value of y when x = 7.
b) Find the value of
x when y = 7.
c) Estimate the value of y when
x = 1.5.
|
|
|
39.
|
A box contains 8 candies. The candies have to be shared between Cam and Kathy.
Let c represent the number of candies Cam gets and k represent the number that
Kathy gets. An equation for this relation is 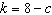 . a) Create a table of values for the
relation.
b) Graph the relation.
c)
Which ordered pair suggests the fairest way to share the candies?
|
|
|
40.
|
a) Graph each
relation for integer values of x from -3 to 3.
b) Which graphs
go up to the right? Which graphs go down to the right?
c) How can
you use the equation of a linear relation to tell if its graph goes up or goes down to the
right?
|